Can you bias a coin?
Challenge: Take a coin out of your pocket. Unless you own some exotic currency, your coin is fair: it’s equally likely to land heads as tails when flipped. Your challenge is to modify the coin somehow—by sticking putty on one side, say, or bending it—so that the coin becomes biased, one way or the other. Try it!
How should you check whether you managed to bias your coin? Well, it will surely involve flipping it repeatedly and observing the outcome, a sequence of h‘s and t‘s. That much is obvious. But what’s not obvious is where to go from there. For one thing, any outcome whatsoever is consistent both with the coin’s being fair and with its being biased. (After all, it’s possible, even if not probable, for a fair coin to land heads every time you flip it, or a biased coin to land heads just as often as tails.) So no outcome is decisive. Worse than that, on the assumption that the coin is fair any two sequences of h‘s and t‘s (of the same length) are equally likely. So how could one sequence tell against the coin’s being fair and another not?
We face problems like these whenever we need to evaluate a probabilistic hypothesis. Since probabilistic hypotheses come up everywhere—from polling to genetics, from climate change to drug testing, from sports analytics to statistical mechanics—the problems are pressing.
Enter significance testing, an extremely popular method of evaluating probabilistic hypotheses. Scientific journals are littered with reports of significance tests; almost any introductory statistics course will teach the method. It’s so popular that the jargon of significance testing—null hypothesis, $p$-value, statistical significance—has entered common parlance.
As common as it is, significance testing is controversial. Some people argue that the method needs to be used with caution; a plug-and-play approach will lead us astray. Others go further, arguing that significance tests are bunk: that the result of a significance test is no guide to the truth of the hypothesis being tested. Colin Howson and Peter Urbach put the claim forcefully:
[Significance tests] are advocated in hundreds of books that are recommended texts in thousands of institutions of higher education, and required reading for hundreds of thousands of students. [Yet] judgments of ‘significance’ and ‘non-significance’ carry no inductive meaning at all. Therefore they cannot be used to arbitrate between rival theories or to determine practical policy.
(Howson and Urbach, 2006: 181–2)
Strong stuff! This post focuses on one objection to significance testing: that significance tests are sensitive to the stopping rule.
First, we’ll see how significance tests work. Then we’ll show that they are sensitive to the stopping rule. And finally we’ll look at some of the back and forth on whether sensitivity to the stopping rule is a problem.
Primer on probability
This section reviews some facts about probability needed later. We’ll work up to solving the following problem: What’s the probability of getting $m$ heads in $n$ flips of a coin, where the probability of heads on any given flip is $q$? If you already know what this is, jump to the next section; else, expand the material below.
How significance tests work
A significance test is a method of evaluating a probabilistic hypothesis. How do significance tests work? The procedure itself is quite simple, but the motivation for the procedure is subtle. So let’s build up to it in stages, to understand why it works the way it does.
Building up to a significance test
Remember the coin you modified earlier. We want to evaluate the hypothesis that the coin is fair. Suppose we flip it some number of times, and see that there are many more heads than tails. Does this give us reason to think it’s biased?
This is a tricky question because, as pointed out earlier, a fair coin can produce any outcome—and so can a biased coin (as long as there’s some non-zero chance of it landing heads and tails). In other words, if you flip your coin repeatedly and look at the resulting sequence, you can’t tell for sure whether your coin is fair or biased. To take an extreme case: it’s possible to flip a fair coin 1000 times and get heads every time. That’s the nature of chance.
Still, even though your coin—fair or biased—can produce any outcome, some outcomes are more likely than others, depending on the bias of the coin. Take the extreme case above: the probability of flipping a fair coin 1000 times and getting heads every time is $0.5^{1000}$. That’s small. In decimals, it’s about
0.0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000093326
So if we flip a coin 1000 times and get heads every single time, we might think that the sheer improbability of getting this sequence for a fair coin gives us very good reason to think that the coin isn’t fair. In other words, we might think that if our result is very improbable on the assumption that the coin is fair, we should reject that assumption.
But wait a second. There’s a big problem with this line of thought. Suppose your coin is fair, and suppose you flip it 1000 times and get not a sequence of 1000 heads, but some other sequence of heads and tails, say:
TTHHHTHHTHHTHTHHTHHHHHTT … HHTTTTTTHTHTTTHTHTHHHTHT
What’s the probability of getting this sequence, assuming the coin is fair? Well, it’s $0.5^{1000}$—exactly the same as the chance of getting 1000 heads. A fair coin has an equal chance of getting any particular sequence—the chance of getting any one of them is extraordinarily tiny. But surely not every outcome gives us reason to think the coin is biased.
So the reasoning we just went through can’t be right. We need something stronger than just the claim that our particular result was improbable. But we can modify the reasoning in a way that gets around this worry, by looking not at the result itself, but at properties of the result. We can pick a characteristic of the result—a test statistic—and see how improbable it is to get a result like the one we got, insofar as the test statistic is concerned. Note that this involves a human decision: by picking a test statistic, we’re deciding what to look at when we group results together as “alike”; the numbers aren’t making that decision for us.
For example, we can pick the number of heads as our test statistic. Instead of asking how unlikely it is, assuming the coin is fair, to get the particular sequence of flips we got, we can instead ask how unlikely it is, assuming the coin is fair, to get the number of heads we got. Suppose, for example, that there are 511 heads in the sequence above. The probability, assuming the coin is fair, of getting that many heads, is:
which is 0.01980746048584404.
This goes a long way toward fixing the problem above. A long way, but not all the way, for notice that it’s still very improbable that we get exactly 511 heads—and similarly for any other number of heads. So getting an improbable number of heads can’t by itself be a reason to think the coin is biased.
So we pull one more trick, and ask not whether it was unlikely, assuming the coin is fair, that we get exactly that many heads, but whether it was unlikely, assuming the coin is fair, that we get that many heads, or a more extreme result.
What does “more extreme” mean? There are two obvious ways to go here. One is to say: that many heads, or more; this is called a one-tailed test. The other is to say: that many heads or more, or that many tails or more (in other words, at least as far away from the expected number); this is called a two-tailed test. Which one of these we pick, like which test statistic we pick, is largely a matter of convention. But once we make that decision, we can calculate the chance that a fair coin would give us a result as or more extreme with respect to our test statistic; this is what’s called the $p$-value.
This gives us the traditional significance test, originally formulated by Ronald Fisher: a result gives us reason to reject our hypothesis if its $p$-value is small enough, given some (conventional) choice of test statistic, one- or two-tailed test, and value for “small enough” (called the “size” or “significance level”).
Looking at $p$-values graphically
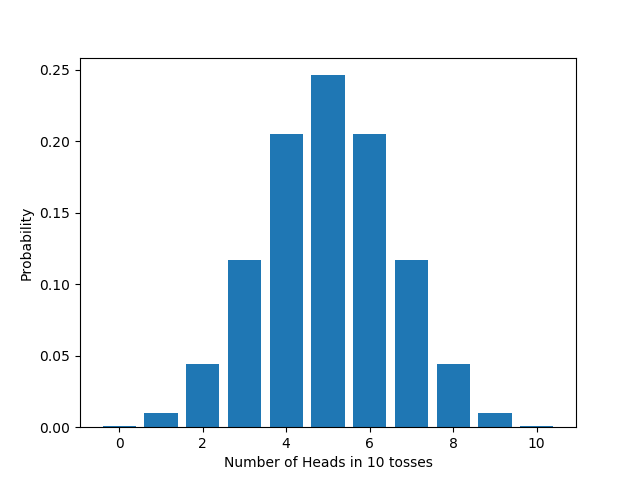
We can put the above reasoning graphically. If we graph the probability of getting any particular sequence, we get a flat distribution if the coin is fair, since each sequence is equally (un)likely:
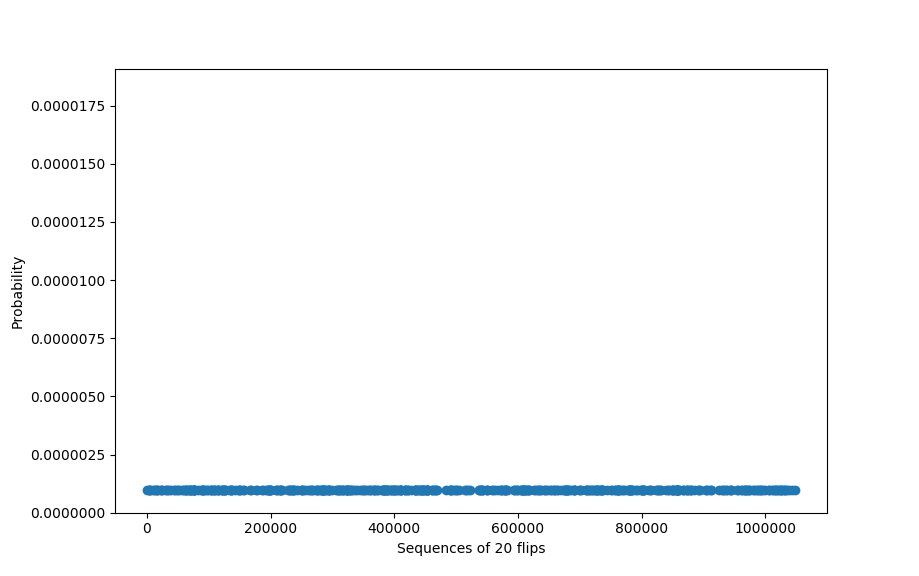
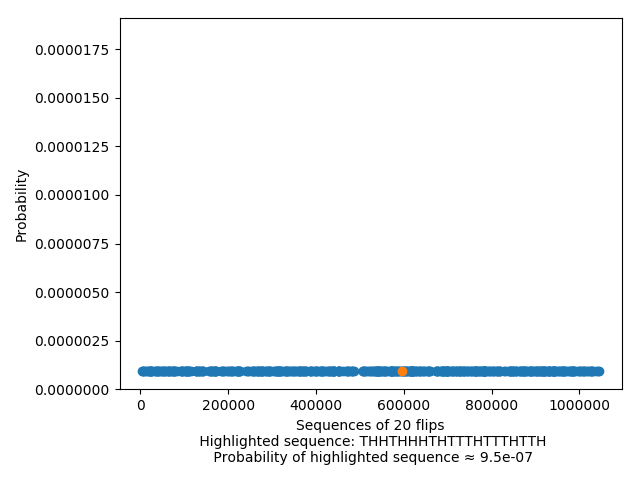
And looking at the chance of any one sequence is just looking at the (tiny, tiny) value of any one of these points:
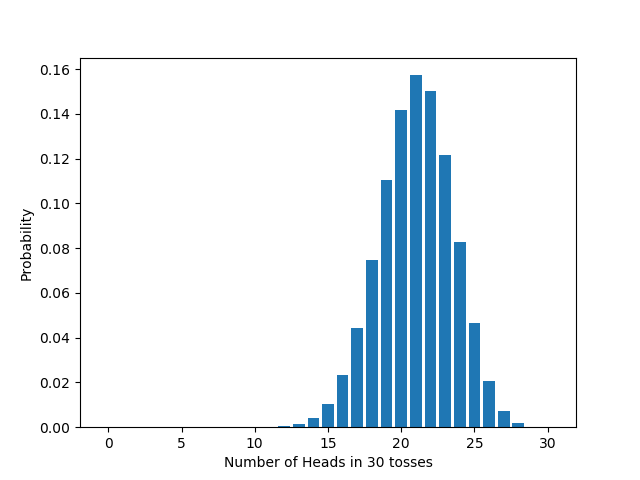
On the other hand, if we look at the distribution of the chosen test statistic, the number of heads, we get the binomial distribution we derived above:
Looking at the likelihood of the test statistic itself amounts to just looking at the likelihood of getting some particular number $m$ of heads:
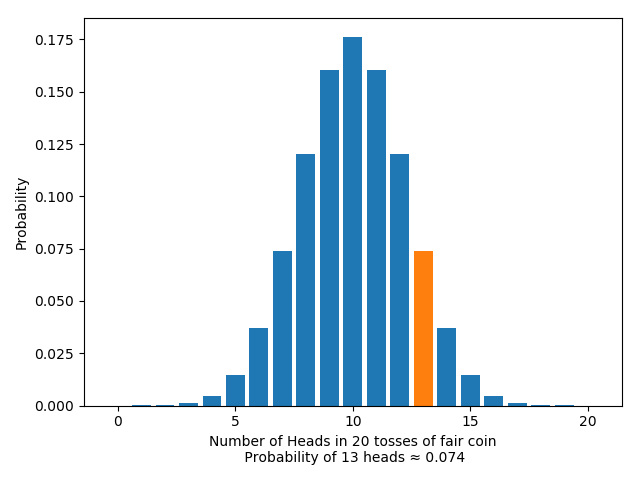
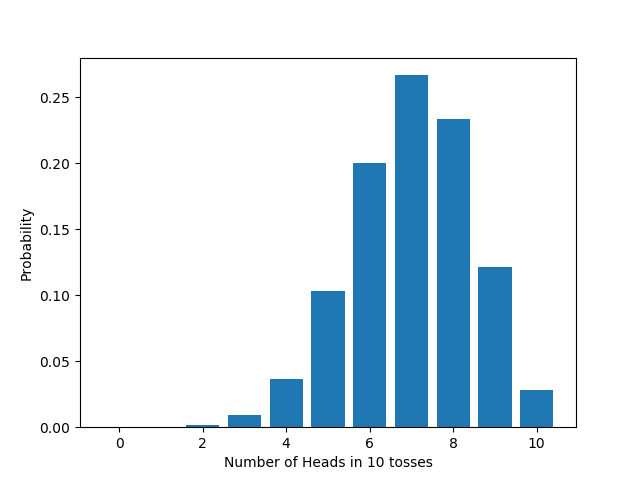
On the other hand, looking at the $p$-value means looking at the likelihood of getting any result as or more extreme than $m$ heads: rather than one single result, we’re looking at the area of an entire region. For the one-tailed test, this looks like:
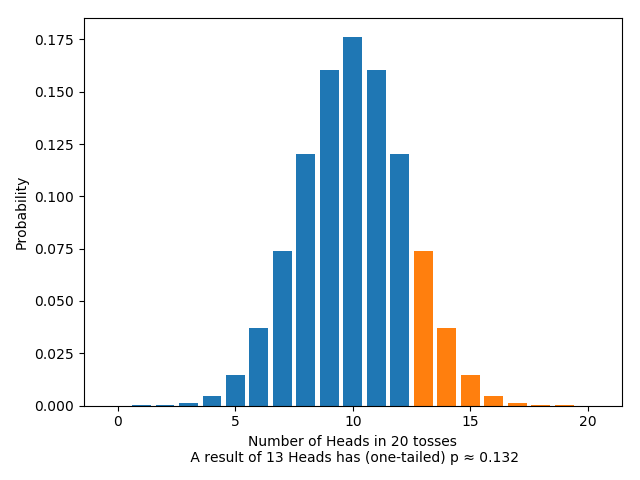
And for the two-tailed test, this looks like:
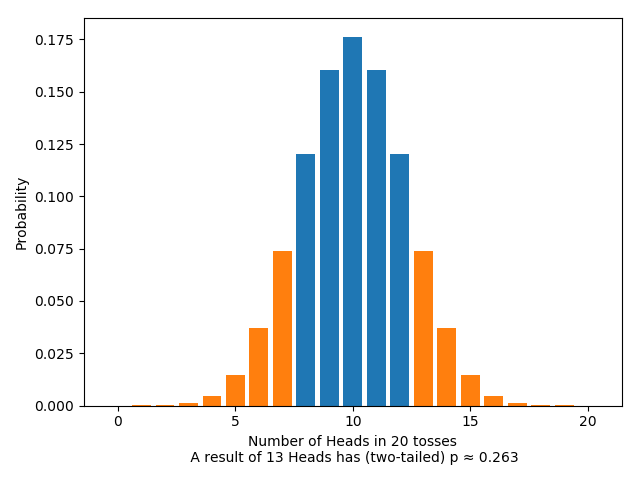
The General Procedure: A Warning
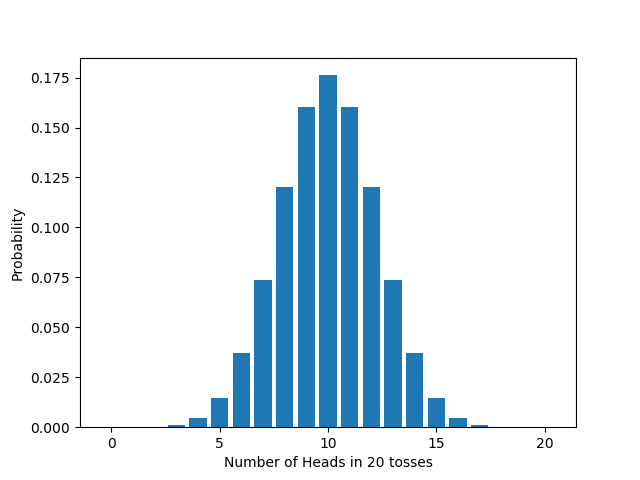
Let’s go over the driving idea behind the test. We want to test whether your coin is fair. Assume for a moment that it is fair. Then if we flip it 20 times, we expect to get about 10 heads. Suppose we actually get 8 heads. That’s not surprising, given our assumption. After all, we only expected to get about 10 heads, not exactly 10 heads. So the result doesn’t call our assumption into question. Suppose instead we actually get 4 heads. To get a result that far from 10 is surprising, given our assumption. So the result does call our assumption into question: either a surprising thing happened or our assumption is wrong. Now, surprising things do happen, but they don’t happen that often, else they wouldn’t be surprising. So the better bet is to reject the hypothesis that the coin is fair. That’s the idea behind significance tests.
In general, suppose we wish to test some probabilistic hypothesis, designated the null hypothesis. Design an experiment and determine all possible experimental outcomes. Then choose a test statistic, which associates a number with each outcome. Assuming that the null hypothesis is true, work out the distribution of the test statistic: that is, for each possible value of the test statistic, work out the probability of getting that value. Next, choose a significance level $\alpha$, typically 0.05 or 0.01, and decide whether to do a one-tailed or two-tailed test. Then do the experiment and note the actual value of the test statistic. Work out the the $p$-value. If the $p$-value is less than $\alpha$, reject the null; else, don’t.
Life would be much easier if the $p$-value of an experiment were the probability that the null hypothesis is true. But it’s not. The truth is more of a mouthful: the $p$-value is the probability of getting a value for the test statistic at least as extreme as the actual value, assuming the null is true. That is quite different to the probability that the null is true.
A lot of technical work has gone into developing significance tests. For example: working out the distribution of a test statistic can be hard and require some sophisticated math; extending the tests to cases where the data is continuous requires further machinery. But the driving idea behind significance tests is simple: do an experiment, and check how extreme the result is, assuming the null.
A different experiment
Suppose we had done our experiment differently: instead of flipping a fixed number of times, we decide we’ll keep flipping until we get a total of 6 tails. This is a perfectly sensible test, because we expect different behaviors from a biased coin and a fair coin: we’d expect a fair coin to take around 12 flips to get 6 tails, a tails-biased coin to do so in fewer flips, and a heads-biased coin to take a longer number of flips. We can even keep the same test statistic: the number of heads will vary between runs, since the length of runs will vary, and the number of heads is always 6 less than the number of flips. We expect around 6 heads for a fair coin. But in this setup, the distribution of the test statistic is different.
What is the distribution? We can work this out from the principles above. Assume the coin has a probability $q$ of getting heads on each flip. If a complete run of our experiments results in $m$ heads, we must have flipped it $m+6$ times, with tails on the final flip. In other words, we get a total of $m$ heads if and only if we got $m$ heads in the first $m+5$ flips, and then a tail. The chance of getting $m$ heads in the first $m+5$ flips is given by the binomial distribution we derived early on: ${m+5 \choose m} (1-q)^5 q^m$. The chance of getting a tail on the final flip is just $1-q$. So the total probability of getting $m$ heads is just ${m+5 \choose m}q^m (1-q)^6$. More generally, the total probability of getting $m$ heads by the time we get $r$ tails is ${m+r -1 \choose m} q^m (1-q)^r.$
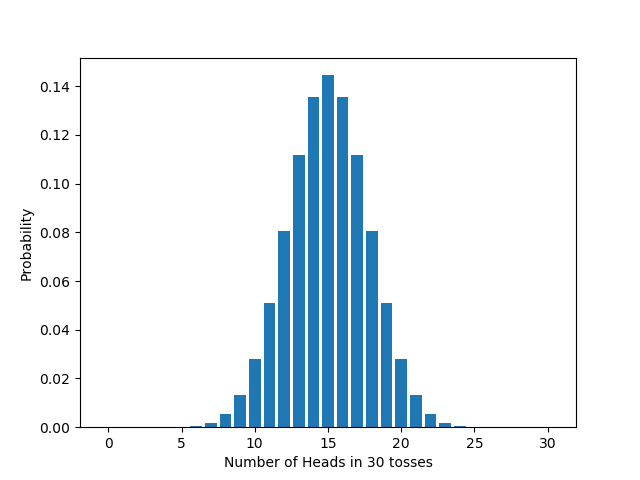
Again, this distribution has a special name: the “negative binomial distribution”. If we graph this distribution for a fair coin ($q=0.5$), it looks like this:
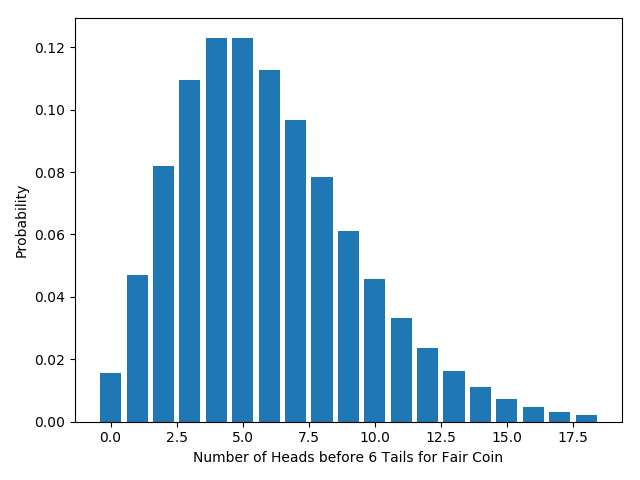
As before, we can calculate the $p$-values (one- and two-tailed) for any given result. For example:
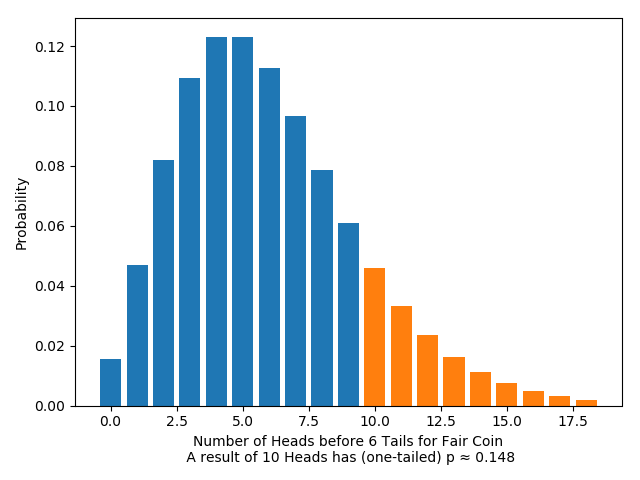
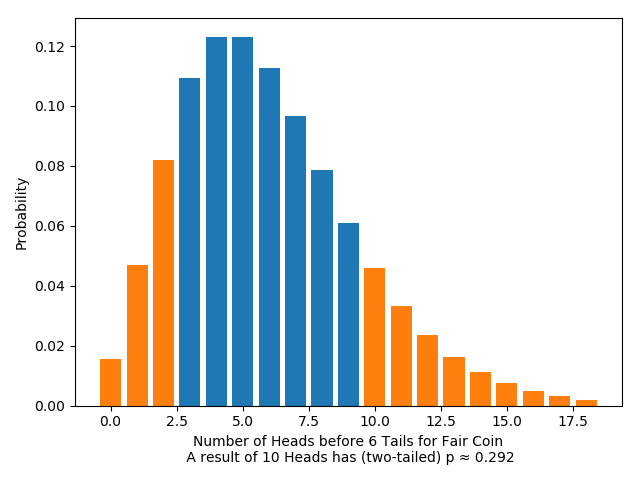
Significance tests are sensitive to the stopping rule
We can express the difference between the two experiments as a difference in when we agree to stop the experiment. In the fixed-number-of-flips experiment, we stop when and only when we reach our target number of flips. In the fixed-number-of-tails experiment, we stop when and only when we reach our target number of tails. In other words, the two experiments have different stopping rules. (Of course, innumerably many other stopping rules are possible too.)
Suppose we perform both experiments: in the fixed-flips experiment we decide to flip a total of 20 times; in the fixed-tails experiment, we decide to flip until we get 6 tails.
Some outcomes are possible in your experiment but not mine, such as a sequence of 9 h‘s and 11 t‘s; other outcomes are possible in mine but not yours, such as a sequence of 8 h‘s and 6 t‘s, ending in a t; but some outcomes are possible in both our experiments, such as hhhththhhhhthhthhhtt, a total of 6 tails, 14 heads.
Let’s do significance tests on the two experiments. As far as our choices of conventions, we’ll pick the same conventions for both: both will test the null hypothesis that the coin is fair; both will use the number of heads as a test statistic; both will use a two-sided test; both will reject the null hypothesis only if the $p$-value is less than $0.05$ (a typical choice). Let’s suppose that, as it happens, we get the same outcome in both experiments, the one at the end of the previous paragraph.
Pulling from the above, for the fixed-flips test we have:
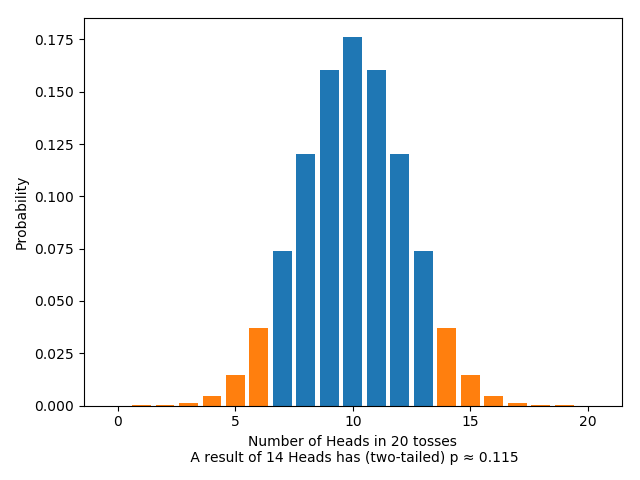
The $p$-value here is greater than $0.05$: according to the test, it’s not a result significant enough to warrant rejecting the null hypothesis that the coin is fair.
At the same time, for the fixed-tails test, we have:
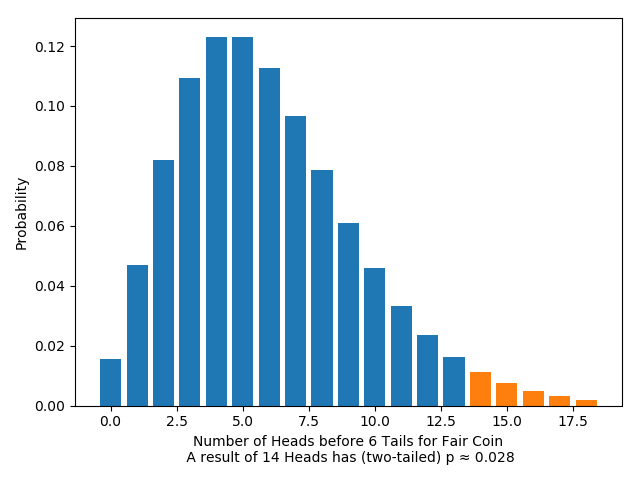
The $p$-value here is less than $0.05$; according to the significance test, this is a result that is significant enough to warrant rejecting the null hypothesis.
But the only difference between the two situations is the stopping rule used! In other words, the very same sequence of coin flips, with the very same conventions, leads to opposite conclusions, depending on which stopping rule was used. That’s what we mean when we say that significance tests are sensitive to the stopping rule.
Is sensitivity to the stopping rule a problem for significance testing?
Plenty of other objections have been leveled at significance tests. But sensitivity to the stopping rule is at the heart of the dispute. Take Deborah Mayo, for example, a staunch defender of significance tests: “Edwards, Lindman, and Savage, quite rightly, regard this difference in attitude on the relevance of stopping rules as a central point of incompatibility between [rival methodologies in statistics].” (Mayo, 1996: 342) Howson and Urbach agree on the centrality of stopping rule sensitivity, although they disagree with Mayo about what conclusion we should draw from it: “The fact that significance tests [are sensitive to the stopping rule] is a decisive objection to the whole approach.” (Howson and Urbach, 2006: 159)
So, then, is sensitivity to the stopping rule a problem for significance testing or not? Examples involving coins can make the question seem academic. Far from it: if stopping rule sensitivity is a problem, we need to know. The question isn’t academic, and nor is it easy. The rest of the post sketches some of the arguments, pro and con. The parts can be read in any order. About half of what I write below is false. But which half?
Irrelevance.
Suppose you do the fixed-flips test and I do the fixed-tails experiment. If someone watches footage of our two experiments, what will she see? She’ll see you flip a coin repeatedly and end up with the sequence hhhththhhhhthhthhhtt; and she’ll see me flip a coin repeatedly and end up with the same sequence. Of course, you intended to flip it 20 times and I intended to flip it until I get a total of 6 tails. But our intentions don’t show up on screen. From our observer’s point of view, our experiments are indistinguishable—until the end, when she’ll see me reject the null and you not.
Fix an hypothesis $H$ and data $D$. Either $D$ is evidence against $H$ or it’s not. In our example, $H$ is that the coin is fair and $D$ is the sequence of coin flips. In my test, $D$ is taken to be evidence against $H$. In your test, it’s not. So one of the tests goes wrong. More generally, whenever a significance test yields one verdict under one stopping rule and another under another, one of the verdicts will be wrong. Therefore, absent any advice about which stopping rules to use, significance tests should not be relied on.
Compare: Suppose I propose a method for evaluating probabilistic hypotheses. The method has a curious property: it’s sensitive to the weather. If it’s raining, a particular experimental outcome is taken to *refute* some hypothesis; if it’s sunny, that same experimental outcome is taken *not* to refute it. Obviously, that’s a vice: no method should be sensitive to the weather. But sensitivity to the stopping rule is no better. No method should be sensitive to anything other than the experimental outcome: same outcome, same inference.
Cheating
Suppose you are an unscrupulous scientist, seeking reason to reject some rival scientist’s hypothesis. Perhaps you can exploit sensitivity to the stopping rule: do a significance test, choosing your stopping rule carefully so as to boost the probability of rejecting the hypothesis.
Take your coin. Suppose I offer a prize if you manage to bias it; I’ll award you the prize if a two-tailed significance test, with test statistic the number of heads, rejects the hypothesis that the coin is fair at a significance level of 5%. You could just do a fixed-flips test, flipping it 20 times, say. But how might you exploit sensitivity to the stopping rule to boost your chances of rejecting the null and winning the prize?
Here’s one attempt: flip the coin until you have 10 more heads than tails. Actually, let’s add a cut-off: flip the coin until you have 10 more heads than tails *or* you’ve flipped it a total of 100 times, whichever comes first. (Adding the cut-off simplifies the analysis; but we could make the same point even if we dropped it.) Call this the *fixed-difference* stopping rule. By choosing the fixed-difference rule, you’ve considerably boosted the probability that you’ll get 10 more heads than tails. So haven’t you also boosted your chances of rejecting the null?
Let’s work it through. First, take the fixed-flips test. When will we reject the null? Well, if we observe no heads at all, we’ll get a *tiny* $p$-value ($2 \cdot \frac{1}{2^{20}}$), so reject. If we observe 1 head, we’ll get a slightly bigger, but still tiny, $p$-value, and still reject. Calculating $p$-values in turn for each possible number of heads, it turns out we reject if the number of heads is between 0 and 5 or 15 and 20, inclusive. So the probability that we reject is the probability that we get between 0 and 5 heads or 15 and 20 heads, inclusive. Assuming the null is true, that’s about 4.1%.
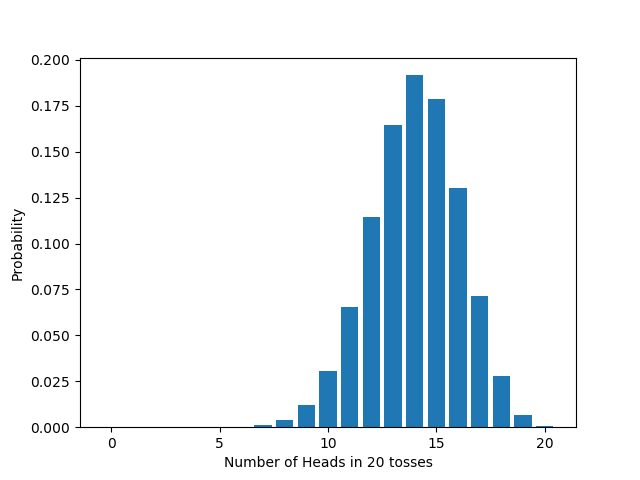
What about the fixed-difference test? This is more complicated. In the fixed-flips test, we can get any number of heads from 0 to 20; but in the fixed-difference test, we can get any number of heads from 0 to 55. (Exercise: Why can’t we get more than 55 heads?) To derive the distribution takes some work (if you’re interested, google “simple random walk”), but here’s the graph:
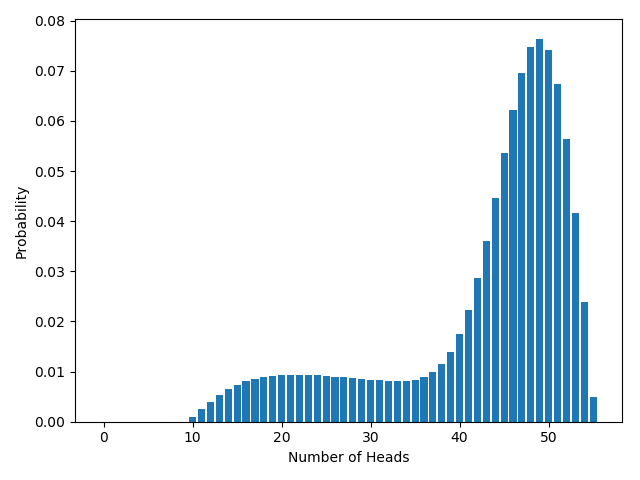
When will we reject the null? Calculating $p$-values in turn for each possible number of heads, as before, it turns out we reject if the number of heads is between 0 and 17, inclusive. So the *probability* that we reject is the *probability* that we get between 0 and 17 heads, inclusive. Assuming the null is true, that’s about 4.3%.
So, admittedly, with the fixed-difference rule we have a slightly higher chance of rejection than with the fixed-flips rule. But the difference is small (4.3% v. 4.1%). That sort of fluctuation isn’t surprising. For example, the chance of rejection in a fixed-flips test where you flip it 20 times is slightly different to the chance of rejection in a fixed-flips test where you flip it 30 times, which is slightly different again to the chance of rejection in a fixed-flips test where you flip it 40 times. Whenever you change your stopping rule, a small fluctuation in the chance of rejection is to be expected. The key point is that when you moved from fixed-flips to fixed-difference, the chance of rejection was pretty much the same; you certainly didn’t significantly boost your chance of rejecting the null, as you hoped.
There’s no deep mystery here. When we moved from fixed-flips to fixed-difference, we *did* boost the chance of observing 10 more heads than tails; in the fixed-flips test, observing 10 more heads than tails (i.e. 15 heads and 5 tails) leads us to reject the null. *but in the fixed-difference test, it doesn’t.* Why not? Because changing the stopping rule also changes the distribution of the test statistic, and so changes which values for the test statistic lead to rejection. What you’ve gained on the swings, you’ve lost on the roundabouts. In fact, it’s straightforward to show that in any significance test, the chance of rejection, assuming the null, is at most the significance level. Change the stopping rule however you like, you won’t boost the chance of rejection above 5%.
Rarity
Even if sensitivity to the stopping rule is a problem, doesn’t it show up only rarely? After all, in our coin example, it’s unlikely that you and I will get the same outcome, so it’s unlikely that the sensitivity to the stopping rule will actually come up in practice.
Agreed: it’s unlikely that you and I will get the same outcome in the coin example. But our two stopping rules do not exhaust the possibilities. The space of possible stopping rules is large. Given that, surely for almost all outcomes in almost all experiments, there are stopping rules such that one leads to rejection and the other doesn’t.
Probability of false rejection
Imagine a machine that plays Tetris. The machine plays well. In fact, the engineer provides a performance guarantee. Since Tetris has a random element—the order and orientation of the falling blocks—the engineer can’t guarantee that the machine *always* gets a score over 100. It might be unlucky. But the engineer can provide a *probabilistic* performance guarantee: with probability 95%, the machine gets a score over 100.
After a while, you notice a strange fact: a copy of the machine in Cambridge and a copy of the machine in Oxford play simultaneously, and by chance the blocks in the two games fall in the same order and orientation. But the machines behave differently. It ends up that the machine in Cambridge gets a score over 100 but the machine in Oxford gets a score less than 100. When you inspect the code, it turns out that the behavior of the machine is sensitive to something surprising: whether it’s raining where the machine is. If it is raining, the machine behaves one way; if it’s not, the machine behaves another. Still, the engineer’s performance guarantee is true: if it’s raining, the machine gets a score over 100 with probability 95%; similarly if it’s not raining; so similarly overall.
Significance tests, so the thought goes, are like the Tetris machine. They also come with a probabilistic performance guarantee: if you do a significance test with significance level 5%, then with probability 95% you won’t reject the null when it’s true. That is a virtue of significance tests: the probability of mistakenly rejecting the null is low. Just as the Tetris machine is sensitive to the weather, so too the significance test is sensitive to the stopping rule. But in neither case does that sensitivity undermine the performance guarantee. No matter the stopping rule, the probability of mistakenly rejecting the null is low. Isn’t that recommendation enough?
Relevance
Suppose you have two experiments: in the first, the experimenter flips the coin until he gets more heads than tails; in the second, the experimenter flips the coin 101 times. Both get the same outcome—the very same sequence of h‘s and t‘s. The outcome contains 51 heads and 50 tails and the number of heads exceeds the number of tails only on the last flip. Surely the outcome points in different directions in the two cases. In the first case, you should be more confident than not that the coin is tails-biased. (After all, it took a long time—101 flips—to get more heads than tails.) In the second case, you should be more confident than not that the coin is heads-biased. (After all, there are more heads than tails.) Which way the experimental outcome points depends on the stopping rule. Therefore being sensitive to the stopping rule is a virtue, not a vice.
Stopping rules in practice
Remember the coin example: your stopping rule is to flip it 20 times; mine is to flip it until I get a total of 6 tails. Your stopping rule is perfectly natural; but mine is odd, and isn’t the kind of thing used in practice. Perhaps the stopping rule sensitivity only arises when we bring in these odd stopping rules. Given the stopping rules used in practice, the phenomenon doesn’t arise, so can be safely ignored.
Well, maybe. But it’s not at all obvious that stopping rule sensitivity does only arise with ‘odd’ stopping rules. Besides, even if it’s true, it may not be enough. Perhaps the fact that significance tests are sensitive to stopping rules at all shows that there is something wrong with the methodology. To rest easy just because the phenomenon doesn’t come up in practice is to confuse suppressing a symptom with curing the disease.
Filed Under